The default state model from the Getting
Started article might not adequately fit the observed
rainfall-runoff relationship. In order for the state shifts to be
statistically adequate and informative, the model’s residuals must
adhere to the required checks in plot.hydroState with
pse.residuals = TRUE (uniform and normally distributed with
no trends or auto-correlation). This vignette introduces a suite of
options to adjust the default state model when model residuals do not
meet the checks. Most often, this requires adjusting the shape of the
residual distribution (error.distribution), applying
auto-correlation terms (parameters), or possibly allowing
for change in different model parameters
(state.shift.parameters).
This vignette works through an example comparing the default model
with an adjusted model. It concludes with the introduction of
build.all() function that systematically builds all
possible adjustments in the state model in order to identify the best
performing model.
Load required data
Annual rainfall-runoff models require a data frame with catchment average runoff and precipitation for each year. Load the data into the environment. Ensure there are three columns named “year”, “flow”, and “precipitation”, and verify the units for flow and precipitation are the same (‘mm’, ‘in’, etc.).
Build a hydroState model with an adjusted the state model
While building the model, adjust the state model that better suites
the distribution or auto-correlation within the residuals.
build() provides several options to better define the
rainfall-runoff relationship. When model residuals are not normally
distributed, consider changing the error.distribution to
gamma or normal. If auto-correlation is
present, consider including an AR1, AR2, or
AR3 term within parameters to assume
auto-correlation of 1, 2, or 3 time lags. It is also possible to reduce
auto-correlation by allowing for 3-states rather than two. This is done
by adjusting the transition.graph to equal
matrix(TRUE,3,3). Or the shift could be occurring within a
different model parameter and this adjustment involves specifying the
state.shift.parameters.
Below are four options to adjust the state model to better fit the
model’s residuals. For further details, see build().
-
parameters- includeAR1,AR2, orAR3to assume auto-correlation of 1, 2, or 3 time lags -
state.shift.parameters- adjust the state dependent parameter toa1or one of the auto-correlation terms.
-
error.distribution- adjust the assumed distribution of the model residuals.truc.normal,normal, andgammaare available. -
transition.graph- adjust the model from a 2-state to 3-state. Available options: 1-state =matrix(TRUE,1,1), 2-state =matrix(TRUE,2,2), or 3-state =matrix(TRUE,3,3)
For this example, we compare the default state model and adjusted model. The default state model is first defined. Then an adjusted state model is created that assumes a gamma distribution in the residuals, 2-states, and auto-regressive lag of 2 time-steps.
# Default state model
default.model.annual = build(input.data = streamflow_annual_407211,
parameters = c('a0','a1','std'),
state.shift.parameters = c('a0','std'),
error.distribution = 'truc.normal',
transition.graph = matrix(TRUE,2,2))
# Adjusted state model assuming the residuals are a gamma distribution, AR2, 2-state, a1
adjusted.model.annual = build(input.data = streamflow_annual_407211,
parameters = c('a0','a1','std','AR2'),
state.shift.parameters = c('a0','std'),
error.distribution = 'gamma',
transition.graph = matrix(TRUE,2,2))Fit the models
Fit both models with fit.hydroState(). The negative
log-likelihood value of each model will be shown.
default.model.annual = fit.hydroState(default.model.annual, pop.size.perParameter = 10, max.generations = 500)
#> ... Finished Calibration.
#> Best solution: 40.0121967394132
adjusted.model.annual = fit.hydroState(adjusted.model.annual, pop.size.perParameter = 10, max.generations = 1000)
#> ... Finished Calibration.
#> Best solution: 26.1477164188363Compare models based on AIC
The adjusted model has a lower AIC suggesting it better fits the rainfall-runoff relationship at for this catchment. To validate the adjusted model is the most suitable, lets evaluate the residuals of each model.
Review the residuals
Review the residuals of both models using
plot.hydroState() to determine which model is more adequate
(uniform and normally distributed with no trends or auto-correlation in
the residuals). The following two figures show the adjusted state model
that assumes a gamma distribution of the residuals,
‘adjusted.model.annual’, is more adequate with a Shapiro-Wilks p-value
greater then 0.05 suggesting residuals are normally distributed.
# review residual plots
plot(default.model.annual, pse.residuals = TRUE, siteID = '407211')
plot(adjusted.model.annual, pse.residuals = TRUE, siteID = '407211')
Evaluate the state-shifts
Set the state names relative to a year in the record using
setInitialYear() and evaluat the flow states overtime of
the adjusted model using plot.hydroState(). The year 1991
is selected as the initial year because there is not sufficient
streamflow data for 1990 at this site (Bet Bet Creek - 407211).
# set the reference year to name the states
adjusted.model.annual = setInitialYear(adjusted.model.annual , 1991)
# plot all four plots
plot(adjusted.model.annual)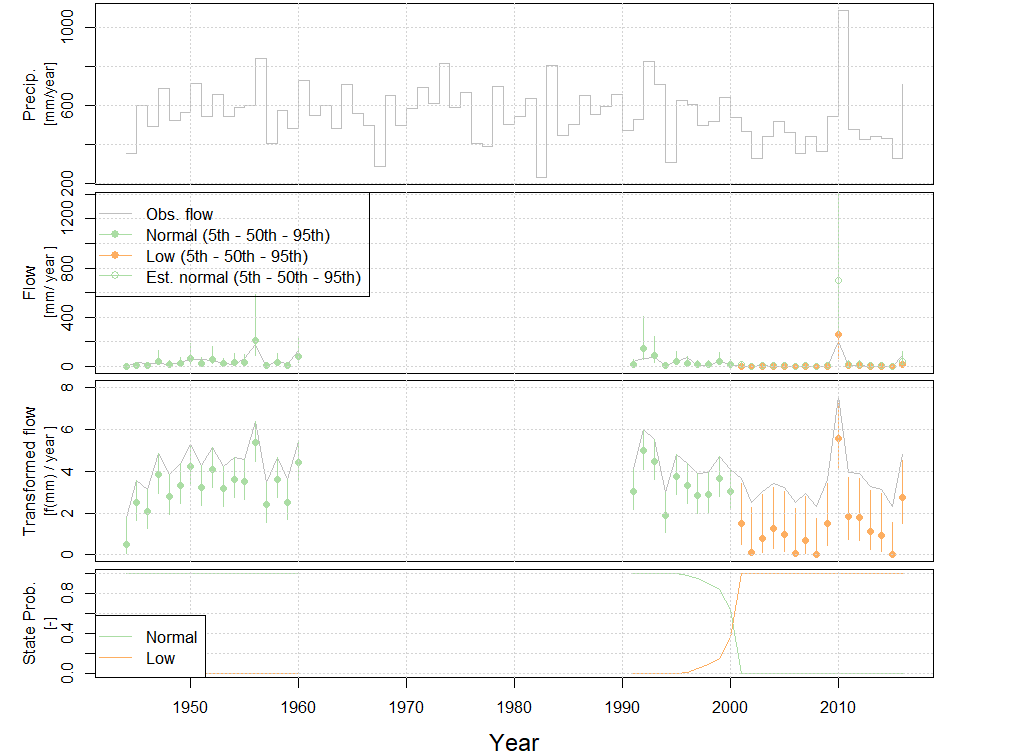
Systematic state model selection
How do we know which state model is the best given our observations?
Rather than manually testing every adjustment of the state model, the
build.all() function builds every possible state model
combination (each distribution, auto-correlation terms, and 1 to
3-states) while the intercept, a0, slope, a1,
or error, std could be considered as
state.shift.parameters. The function performs similarly to
build() and can easily replace this function in the
workflow. After being built, the models can be fitted using the
fit.hydroState function. This function fits each model
iteratively, and requires each model to provide a better fit than the
previous simpler model known as the reference model. Each model
undergoes 20 calibration trials, and if the best model fit of the trails
is not less than or equal to the reference model calibration, the
calibration reference criteria in the list of models is 0. To
see a summary of the order of the reference models and revise them, use
the summary.hydroState.allModels() function. Once the
models are fitted, the best model is the one with the lowest AIC, and
the get.AIC() function outputs a table with each model and
AIC.
Below is a an example of how to set up build.all(), and
perform the steps to adjust the reference table using
summary.hydroState.allModels(), fit the models using
fit.hydroState(), and identify the model with the lowest
AIC. Note, parallel processing is recommended as fitting all models can
take several hours to run.
# Build all model combinations with 'a0' and 'std' as state-dependent parameters
all.models = build.all(input.data = streamflow_annual_407211,
state.shift.parameters =c('a0','std'),
siteID = "407211")
# Review the order of the reference models, adjust reference models if needed.
all.models.ref.table = summary(all.models)
# If reference models are adjusted, then re-build models
all.models = build.all(input.data = streamflow_annual_407211,
state.shift.parameters = c('a0','std'),
summary.table = all.models.ref.table)
# Fit all models (takes hours to run)
<!-- all.models = fit.hydroState(all.models, pop.size.perParameter = 10, max.generations = 5000, doParallel = T) -->
#> Calibrating 36 Models.
#> ... Minimum number of calibration per model: 5
#> ... Maximum number of calibration per model: 20
#> ************************************
#> Calibrating Model: model.1State.truc.normal.boxcox.AR0.a0std
#> Reference model name for maximum acceptable calib. solution:
#> Reference model maximum acceptable calib. solution: -Inf
#> ...
# get table of AIC values for each model
get.AIC(all.models)
#> AIC nParameters
#> model.2State.gamma.boxcox.AR0.a0std 79.36469 8
#> model.2State.gamma.boxcox.AR2.a0std 79.39221 10
#> model.2State.gamma.boxcox.AR3.a0std 81.39029 11
#> model.2State.gamma.boxcox.AR1.a0std 82.48915 9
#> model.1State.gamma.boxcox.AR2.a0std 89.13483 5
#> model.1State.gamma.boxcox.AR3.a0std 91.83986 6
#>...